Circumference Of A Circle Formula Diameter And Radius

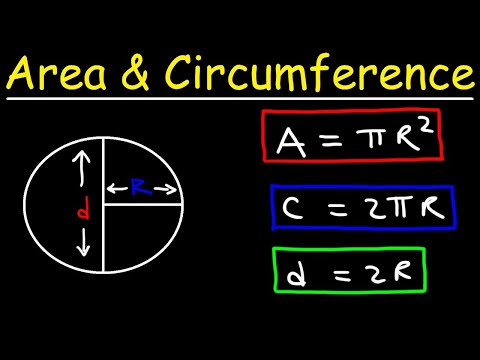
A circle is a geometric form of which every point on the outside of the circle is the same distance away from the center. The distance around the edge of the circle is called the circumference. The distance from one side of the circle to the other, going through the center of the circle, is the diameter. The constant pi, designated by the Greek letter π, is the ratio of the circumference to the diameter of a circle.

For any circle, if you divide the circumference by the diameter you get pi, an irregular number usually rounded to 3.14. We'll teach you the key circumference formulas you need to figure out the circumference of a circle when you know either the diameter or radius. The distance from the centre to the outer line of the circle is called a radius. It is the most important quantity of the circle based on which formulas for the area and circumference of the circle are derived. Twice the radius of a circle is called the diameter of the circle.

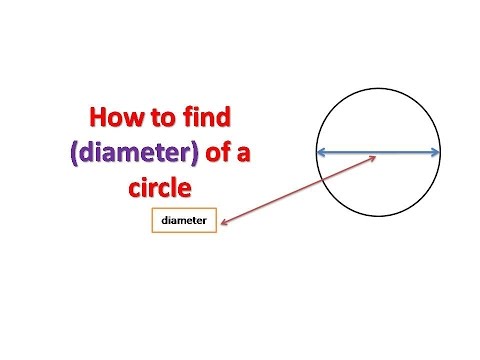
The diameter cuts the circle into two equal parts, which is called a semi-circle. The diameter of the circle is the largest chord and is passing through the center of the circle. The circumference of the circle is the length of the outer boundary of the circle. Both the diameter and the circumference are lengths and have linear units for measurement.

Also, the circumference of the circle is equal to the product of the diameter and the constant pi. The perimeter of a circle is the same as the circumference of a circle. It is the total length of the outer boundary of the circle. The perimeter or circumference of a circle is the product of the constant pi and the diameter of the circle. It is a linear one-dimensional quantity and has units such as m, inch, cms, feet. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye.

While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle.

You can also think of the radius as the distance between the center of the circle and its edge. Once again in this example, we're given the radius of the circle. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m. Although the circumference of a circle is its length, it cannot be calculated with the help of a ruler like it is usually done for other polygons. This is because a circle is a curved figure.

The circumference of a circle is the perimeter of the circle. It is the total length of the boundary of the circle. The circumference of a circle is the product of the constant π and the diameter of the circle. A person walking across a circular park, or a circular table to be bordered requires this metric of the circumference of a circle.

The circumference is a linear value and its units are the same as the units of length. Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. Then, find your radius, and circumference.

Perimeter of other shapes like squares. You can think of it as the line that defines the shape. For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference.

Π shows the ratio of the perimeter of a circle to the diameter. Therefore, when you divide the circumference by the diameter for any circle, you obtain a value close enough to π. This relationship can be explained by the formula mentioned below. Pi (π) is a special mathematical constant; it is the ratio of circumference to diameter of any circle. When we use the formula to calculate the circumference of the circle, then the radius of the circle is taken into account.

Hence, we need to know the value of the radius or the diameter to evaluate the perimeter of the circle. Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of circle defines the region occupied by it. If we open a circle and make a straight line out of it, then its length is the circumference. It is usually measured in units, such as cm or unit m. Pi is a constant value used for the measurement of the area and circumference of a circle or other circular figures.

The symbol of pi is π and its numeric value is equal to 22/7 or 3.14. Further, these numeric values are used based on the context of the equation. The circumference of a circle is defined as the linear distance around it. In other words, if a circle is opened to form a straight line, then the length of that line will be the circle's circumference. We know that the diameter of a circle is twice the radius. The proportion between the circumference of a circle and its diameter is equal to the value of Pi(π).

Hence, we say that this proportion is the definition of the constant π. Now, let's take the circle with the diameter of 9 cm, and radius of 4.5 cm, and calculate the circumference. The distance around a rectangle or a square is as you might remember called the perimeter. The distance around a circle on the other hand is called the circumference . Thus, we can define three different formulas to find the perimeter of circle (i.e. circumference of a circle).

The circumference of the circle is a one-dimensional linear quantity and it has the same units of that of the length. The units of the circumference of a circle could be m, inch, cm, feet. The circumference of a circle is related to other linear quantities such as the radius, and diameter of the circle. The circumference of a circle is its boundary or the length of the complete arc of a circle. The circumference of the circle is the product of π a constant and d the diameter of the circle. The circumference of a circle is a linear quantity that has the same units of length.

The circumference of a circle refers to the measure of its boundary. If a boy starts running from point 'A' and reaches the same point after taking one complete round of the park, a distance is covered by him. This distance or boundary is called the circumference of the park which is in the shape of a circle. The circumference is the Length of the Boundary. Circumference is the distance around the perimeter of a circle.

It is calculated by multiplying the distance across the center by Pi (3.1416). Since a circle's circumference is the linear distance of the circle's edge, it describes a length. The circumference of a circle is the linear distance of the circle's edge. It is equivalent to the perimeter of a geometric shape, although that term perimeter is only used for polygons. Either of these circumference formulas can be used to help you solve problems.

Learn to find the diameter or radius of a circle given the circumference. So, the diameter of the circle in terms of circumference will be equal to the ratio of the circumference of the circle and pi. But, what if we aren't given either of these values?

In order to solve for either the radius or diameter of a circle, we need to know either its circumference or its area. The easiest thing to start with would be to take the ruler and measure, from the very center of the circle, the length between the outer edge. But let's say we wanted to find the radius, diameter, and circumference of that circle, and all we have is a ruler.

Things like radius, diameter, and circumference are terms that helps us to keep track of various measurements of a circle. The first technological invention using a circular shape, however, wasn't until 3500 BC, and it was the invention of the potter's wheel. Then, 300 years later, they were used for the wheels of chariots. As people began to see the value and use for circular-shaped objects, they begin to study circles.

Understanding what a circumference of a circle is and how to calculate it is crucial as you move to higher level math. In this article you will learn the answers to the following questions. Divide the circumference by π, or 3.14 for an estimation. The result is the circle's diameter, 3.18 centimeters. This is the circle's diameter, in this case, 31.8 centimeters. Use our circumference calculator to find the radius when you only have the circumference or area of a circle.

Our goal is to make science relevant and fun for everyone. Divide the circumference by pi to get the answer. In this case, the diameter would be 3.82 inches. Feel free to play around with this online circle calculator to see how the circumference changes as the diameter and radius changes. We'll do a three examples to help you learn how to find the circumference of a circle using the formulas we just learned. Calculate the perimeter of circle whose diameter is 8 cm.

A circle is defined as a shape with all the points are equidistant from a point at the centre. The circle depicted below has its centre lies at point A. In Mathematics, the circumference of any shape defines the path or the boundary that surrounds the shape.

In other words, the circumference is also called the perimeter, which helps to identify the length of the outline of any shape. A Circle is a round closed figure where all its boundary points are equidistant from a fixed point called the center. The two important metrics of a circle is the area of a circle and the circumference of a circle.

Here we shall aim at understanding the formula and calculation of the circumference of a circle. Determine the radius of the circle if the circumference is twenty-three inches. Round your answer to the nearest hundredths. If you remember only one fact about circles, let this one be it.

A radius is half the length of the diameter. Now, you may be asking, "Well where did pi come from, and why do we all the sudden get the circumference if we multiply said pi by our diameter? " If you are not asking that question… You should, and I'm going to answer it anyways.

Now that we've looked at what the radius, diameter, and circumference are, let's look at how to calculate each one. Circumference is comparable to the perimeter of a shape, like a parallelogram. If you were to cut the line of a circle, as if it were a string, and lay it out to measure. This length would be equivalent to the circumference. However, since a circle has a continuous curve, we use the word circumference rather than perimeter to distinguish it.

Square the radius, and multiply by pi. Double the radius to get the diameter. Then multiply by pi to get the circumference. The perimeter of a circle is the same as its circumference, the distance around it. The term "perimeter" refers to the distance around any closed shape, and "circumference" applies specifically to a circle or arc. Half of the diameter, or the distance from the midpoint to the circle border, is called the radius of the circle .

Have you ever wondered how big the earth is? Well, using pi it's possible to work out the circumference of the Earth! Scientists have discovered that the diameter of the Earth is 12,742km.

Given this information, what is the circumference of the Earth? Get out a piece of paper and a calculator and see if you can work it out on your own. The first person to calculate the Earth's circumference was Eratosthenes, a Greek mathematician, in 240 B.C. Knowing this, and the distance between the locations, he succeeded in calculating the Earth's circumference. This proportion is the definition of the constant pi. It is used in many areas, such as physics and mathematics.

For example, you can find it in the centrifugal force calculator. If DF is the diameter of circle C, find its length. Generally, it's easier to use whichever formula corresponds with the characteristics of the circle you are given. The semi-circle is formed when we divide the circle into two equal parts. Therefore, the perimeter of the semi-circle also becomes half.