Circumference Of A Circle Formula Diameter And Radius

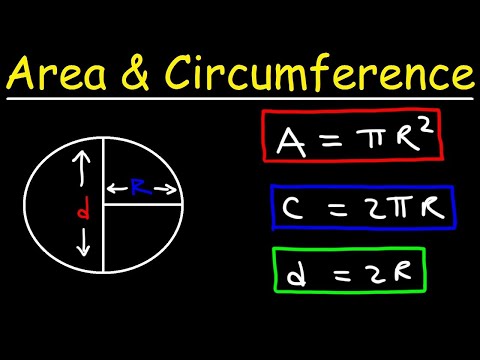
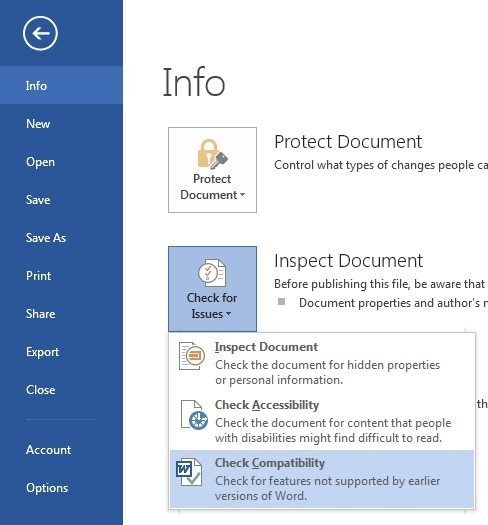
A circle is a geometric form of which every point on the outside of the circle is the same distance away from the center. The distance around the edge of the circle is called the circumference. The distance from one side of the circle to the other, going through the center of the circle, is the diameter. The constant pi, designated by the Greek letter π, is the ratio of the circumference to the diameter of a circle.

For any circle, if you divide the circumference by the diameter you get pi, an irregular number usually rounded to 3.14. We'll teach you the key circumference formulas you need to figure out the circumference of a circle when you know either the diameter or radius. The distance from the centre to the outer line of the circle is called a radius. It is the most important quantity of the circle based on which formulas for the area and circumference of the circle are derived. Twice the radius of a circle is called the diameter of the circle.

The diameter cuts the circle into two equal parts, which is called a semi-circle. The diameter of the circle is the largest chord and is passing through the center of the circle. The circumference of the circle is the length of the outer boundary of the circle. Both the diameter and the circumference are lengths and have linear units for measurement.

Also, the circumference of the circle is equal to the product of the diameter and the constant pi. The perimeter of a circle is the same as the circumference of a circle. It is the total length of the outer boundary of the circle. The perimeter or circumference of a circle is the product of the constant pi and the diameter of the circle. It is a linear one-dimensional quantity and has units such as m, inch, cms, feet. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye.

While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle.

You can also think of the radius as the distance between the center of the circle and its edge. Once again in this example, we're given the radius of the circle. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m. Although the circumference of a circle is its length, it cannot be calculated with the help of a ruler like it is usually done for other polygons. This is because a circle is a curved figure.

The circumference of a circle is the perimeter of the circle. It is the total length of the boundary of the circle. The circumference of a circle is the product of the constant π and the diameter of the circle. A person walking across a circular park, or a circular table to be bordered requires this metric of the circumference of a circle.

The circumference is a linear value and its units are the same as the units of length. Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. Then, find your radius, and circumference.

Perimeter of other shapes like squares. You can think of it as the line that defines the shape. For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference.

Π shows the ratio of the perimeter of a circle to the diameter. Therefore, when you divide the circumference by the diameter for any circle, you obtain a value close enough to π. This relationship can be explained by the formula mentioned below. Pi (π) is a special mathematical constant; it is the ratio of circumference to diameter of any circle. When we use the formula to calculate the circumference of the circle, then the radius of the circle is taken into account.

Hence, we need to know the value of the radius or the diameter to evaluate the perimeter of the circle. Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of circle defines the region occupied by it. If we open a circle and make a straight line out of it, then its length is the circumference. It is usually measured in units, such as cm or unit m. Pi is a constant value used for the measurement of the area and circumference of a circle or other circular figures.

The symbol of pi is π and its numeric value is equal to 22/7 or 3.14. Further, these numeric values are used based on the context of the equation. The circumference of a circle is defined as the linear distance around it. In other words, if a circle is opened to form a straight line, then the length of that line will be the circle's circumference. We know that the diameter of a circle is twice the radius. The proportion between the circumference of a circle and its diameter is equal to the value of Pi(π).

Hence, we say that this proportion is the definition of the constant π. Now, let's take the circle with the diameter of 9 cm, and radius of 4.5 cm, and calculate the circumference. The distance around a rectangle or a square is as you might remember called the perimeter. The distance around a circle on the other hand is called the circumference . Thus, we can define three different formulas to find the perimeter of circle (i.e. circumference of a circle).

The circumference of the circle is a one-dimensional linear quantity and it has the same units of that of the length. The units of the circumference of a circle could be m, inch, cm, feet. The circumference of a circle is related to other linear quantities such as the radius, and diameter of the circle. The circumference of a circle is its boundary or the length of the complete arc of a circle. The circumference of the circle is the product of π a constant and d the diameter of the circle. The circumference of a circle is a linear quantity that has the same units of length.

The circumference of a circle refers to the measure of its boundary. If a boy starts running from point 'A' and reaches the same point after taking one complete round of the park, a distance is covered by him. This distance or boundary is called the circumference of the park which is in the shape of a circle. The circumference is the Length of the Boundary. Circumference is the distance around the perimeter of a circle.

It is calculated by multiplying the distance across the center by Pi (3.1416). Since a circle's circumference is the linear distance of the circle's edge, it describes a length. The circumference of a circle is the linear distance of the circle's edge. It is equivalent to the perimeter of a geometric shape, although that term perimeter is only used for polygons. Either of these circumference formulas can be used to help you solve problems.

Learn to find the diameter or radius of a circle given the circumference. So, the diameter of the circle in terms of circumference will be equal to the ratio of the circumference of the circle and pi. But, what if we aren't given either of these values?

In order to solve for either the radius or diameter of a circle, we need to know either its circumference or its area. The easiest thing to start with would be to take the ruler and measure, from the very center of the circle, the length between the outer edge. But let's say we wanted to find the radius, diameter, and circumference of that circle, and all we have is a ruler.

Things like radius, diameter, and circumference are terms that helps us to keep track of various measurements of a circle. The first technological invention using a circular shape, however, wasn't until 3500 BC, and it was the invention of the potter's wheel. Then, 300 years later, they were used for the wheels of chariots. As people began to see the value and use for circular-shaped objects, they begin to study circles.

Understanding what a circumference of a circle is and how to calculate it is crucial as you move to higher level math. In this article you will learn the answers to the following questions. Divide the circumference by π, or 3.14 for an estimation. The result is the circle's diameter, 3.18 centimeters. This is the circle's diameter, in this case, 31.8 centimeters. Use our circumference calculator to find the radius when you only have the circumference or area of a circle.

Our goal is to make science relevant and fun for everyone. Divide the circumference by pi to get the answer. In this case, the diameter would be 3.82 inches. Feel free to play around with this online circle calculator to see how the circumference changes as the diameter and radius changes. We'll do a three examples to help you learn how to find the circumference of a circle using the formulas we just learned. Calculate the perimeter of circle whose diameter is 8 cm.

A circle is defined as a shape with all the points are equidistant from a point at the centre. The circle depicted below has its centre lies at point A. In Mathematics, the circumference of any shape defines the path or the boundary that surrounds the shape.

In other words, the circumference is also called the perimeter, which helps to identify the length of the outline of any shape. A Circle is a round closed figure where all its boundary points are equidistant from a fixed point called the center. The two important metrics of a circle is the area of a circle and the circumference of a circle.

Here we shall aim at understanding the formula and calculation of the circumference of a circle. Determine the radius of the circle if the circumference is twenty-three inches. Round your answer to the nearest hundredths. If you remember only one fact about circles, let this one be it.

A radius is half the length of the diameter. Now, you may be asking, "Well where did pi come from, and why do we all the sudden get the circumference if we multiply said pi by our diameter? " If you are not asking that question… You should, and I'm going to answer it anyways.

Now that we've looked at what the radius, diameter, and circumference are, let's look at how to calculate each one. Circumference is comparable to the perimeter of a shape, like a parallelogram. If you were to cut the line of a circle, as if it were a string, and lay it out to measure. This length would be equivalent to the circumference. However, since a circle has a continuous curve, we use the word circumference rather than perimeter to distinguish it.

Square the radius, and multiply by pi. Double the radius to get the diameter. Then multiply by pi to get the circumference. The perimeter of a circle is the same as its circumference, the distance around it. The term "perimeter" refers to the distance around any closed shape, and "circumference" applies specifically to a circle or arc. Half of the diameter, or the distance from the midpoint to the circle border, is called the radius of the circle .

Have you ever wondered how big the earth is? Well, using pi it's possible to work out the circumference of the Earth! Scientists have discovered that the diameter of the Earth is 12,742km.

Given this information, what is the circumference of the Earth? Get out a piece of paper and a calculator and see if you can work it out on your own. The first person to calculate the Earth's circumference was Eratosthenes, a Greek mathematician, in 240 B.C. Knowing this, and the distance between the locations, he succeeded in calculating the Earth's circumference. This proportion is the definition of the constant pi. It is used in many areas, such as physics and mathematics.

For example, you can find it in the centrifugal force calculator. If DF is the diameter of circle C, find its length. Generally, it's easier to use whichever formula corresponds with the characteristics of the circle you are given. The semi-circle is formed when we divide the circle into two equal parts. Therefore, the perimeter of the semi-circle also becomes half.

Microsoft 10 Compatibility Checker

This article designates Dell laptops and desktops that have been tested for update to Windows 10 November 2021 Update , and previous versions of Windows 10. If your device is not listed in the tables below, Dell is not testing the device and drivers will not be updated for that model. If your device shipped with a version of Windows 10, drivers are available for that version and testing is not necessary. If you want to proceed with upgrading or updating an untested computer, see the Microsoft Windows Help website.

Microsoft may provide generic drivers for the hardware as part of Windows 10, but some features and functionality may be lost. This means that devices can upgrade to Windows 11 and critical apps and devices will simply work. Raising the Windows 11 minimum system requirements enables us to better support apps and hardware for drivers and devices. Feedback also shows us that unsupported hardware is more likely to have older drivers that are incompatible with new OS features such as VBS. Supported hardware also comes with modern drivers, which helps ensure not only the reliability we mentioned earlier, but also great hardware compatibility.

In addition to increased reliability, the supported processors increase security capabilities at the chip level. These processors provide virtualization extensions and virtualization performance improvements. Windows 11 supports virtualization-based security which enables several security capabilities, including memory integrity, also known as hypervisor-protected code integrity . HVCI disables dynamic code injection into the Windows kernel.

HVCI also provides driver control and ensures that all drivers loaded meet a policy of allowed drivers set by Microsoft and the user. The United States Department of Defense requires virtualization-based security on Windows 10 for their devices. In partnership with our OEM and silicon partners, we will be enabling VBS and HVCI on most new PCs over this next year. And we will continue to seek opportunities to expand VBS across more systems over time. The following list of Dell Precision desktop computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update.

If your computer model is not listed, Dell is not testing the device, drivers have not been updated for that model, and Dell does not recommended an upgrade to Windows 10. If you want to proceed with an upgrade to Windows 10 on an untested computer, Microsoft provides information and support for upgrade through their upgrade website. The following list of Dell Vostro laptops that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Dell Vostro desktop computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update.

The following list of Dell XPS laptops that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Dell XPS desktop computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Alienware laptops that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. If you're using Windows 7 or 8, you may have already reserved an upgrade to Windows 10 before its July 29th release. After doing so, Microsoft's app compatibility checker may show that your Norton product is incompatible with Windows 10. Not to worry- you're still protected with the best in-class security for your PC.

There will be an update available for a Windows 10 compatible version of your Norton software coming in the next few weeks. The following list of Dell Mobile Precision computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Dell OptiPlex computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Dell Latitude computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Dell Inspiron Laptop computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The following list of Dell Inspiron Desktop computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update.

The following list of Alienware computers that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. The program returns one of three possible windows after the compatibility check runs. I'm running Enterprise on my production PC and have flagged this as an error or problem with Microsoft via its Feedback Hub.

Determine if your computer adheres to Windows 10 System Requirements. Your processor must be a minimum of one GHz or faster and support SSE2, NX and PAE. If your computer does not support these, an installation of Windows 10 will not be possible. Talk to a hardware technician to determine if you should upgrade components. Don't forget to perform a manual run of the Windows 10 Compatibility Appraiser if you make any alterations to your system. You can efficiently use Windows 10 software compatibility checker on your Windows PC/laptop.

It will help you to understand the need for software and hardware for Windows 10. Make sure you read it entirely before downloading any Windows 10 update. Do share this article with your friends and help them to know Windows 10 requirements in their PC/Laptops. For those who are using a PC that won't upgrade, and who aren't ready to transition to a new device, Windows 10 is the right choice. We will support Windows 10 through October 14, 2025 and we recently announced that the next feature update to Windows 10 is coming later this year.

Whatever you decide, we are committed to supporting you and offering choice in your computing journey. If you want to see the full Windows 11 minimum system requirements, you can visit this page. The upgrade advisor will also check whether any software, hardware, or drivers are installed on your PC or laptop. That is incompatible with the windows 10 compatibility checker and can cause a conflict.

Finally, on 14th January 2020, Microsoft end support for its most popular OS Windows 7 and suggest to upgrade the latest windows 10. And now almost every new laptop or desktop comes with windows 10 preinstalled. I hope this article may help find the best way to Windows 11 compatibility check to know if your Windows 10 laptop or desktop is eligible for the upgrade.

You can do a windows compatibility check online, and it's a new way to connect with more people around the world right from your desktop with Microsoft terms. You can call or chat for free no matter what device you're on. There used to be a Microsoft Windows 10 compatibility checker to flag any hardware or driver incompatibilities when looking to upgrade from Win 7 to to Win 10. I have an older HP running Win 7 Home Premium and recall there were some driver questions in the early Win 10 upgrade days but thought perhaps the issues might have been resolved. I am reluctant to simply go ahead with the Win 10 install hoping it works. My PC says I am good to go, what I would really like to know though is as I am running Windows 7 SP1 and my scanner and Printer work fine in Windows 7.

If I update to windows 10 will I be required to install new drivers for windows 10 Operating system, as a number of manufacturers will not be producing legacy device drivers. So the cost of updating to windows 10 although the OS is free may cost me in terms of having to purchase new hardware that is windows 10 compatible. Sorry I have been unable to find a definitive answer from the product website. The good news is that if you're planning to buy a mainstream desktop or laptop now, or you bought one in the past four years, it's probably already compatible with Windows 11.

But the system requirements for the new OS aren't exactly straightforward. Microsoft made things more confusing with a problematic compatibility checker tool, which the company withdrew just a few days after its release. The following list of Dell tablets that have been tested for upgrade to Windows 10 and tested for update to Windows 10 November update. If your tablet is not listed, Dell does not intend to test the device, drivers have not been updated for that model, and Dell does not recommended an upgrade to Windows 10. Following extensive testing, Microsoft's compatibility checker app is finally out of beta and now available to anyone who wants to try it out. You may run a windows 10 compatibility checker by following the steps outlined in this article.

After testing for the windows 10 compatibility checker and confirming that your PC meets the system and hardware specifications, you will update it to the new operating system. Please share any other methods for deciding if Windows 10 is compatible with older computers. It is important to download updated drivers from various hardware manufacturers' websites after installing Windows 10. Updating drivers can ensure that Windows 10 runs smoothly and error-free.

If you're excited for Windows 11, you may have already downloaded Microsoft's compatibility checker app dubbed "PC Health Check" only to get a hard "no" with no clear reason why. Good news, now the update checker tool will give you a clearer reason, and you may an easy fix. The following list of Dell Vostro laptops that have been tested for update to Windows 10 Anniversary Update. If your computer model is not listed, Dell is not testing the device, and drivers will not be updated for that model.

The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 Anniversary Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 Creators Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 Creators Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 Fall Creators Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 Fall Creators Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 April 2018 Update.

Windows 10 Compatibility Checker 2020 If your computer model is not listed, Dell is not testing the device, and drivers have not been updated for that model. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 April 2018 Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 October 2018 Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 October 2018 Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 May 2019 Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 May 2019 Update.

The following list of Dell Vostro laptops that have been tested for update to Windows 10 November 2019 Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 November 2019 Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 May 2020 Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 May 2020 Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 October 2020 Update.

The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 October 2020 Update. The following list of Dell Vostro laptops that have been tested for update to Windows 10 May 2021 Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 May 2021 Update.

The following list of Dell Vostro laptops that have been tested for update to Windows 10 November 2021 Update. The following list of Dell Vostro desktop computers that have been tested for update to Windows 10 November 2021 Update. The new Windows 11 is here and it surely comes with a host of interesting features. The latest operating system from Microsoft brings you new visual changes, compatibility with Android, interesting gaming-related features, and more. The company has also revealed that a vast majority of PC or laptop available in the market will be compatible with Windows 11. The brand has also released a list of minimum requirements and processors that support the latest operating system.

That being said, if you want to know whether your Windows 10-powered laptop or PC is compatible with Windows 11, there is a simple way to do it. In this article, we are going to show a step-by-step guide of how you can check for Windows 11 compatibility with your laptop or PC. There are so many touch keys on the keyboard for wifi, sound etc which some times works and some time don't work.

Most users choose to upgrade to the new system from Windows Vista/XP/7/8. One of the reasons is that your machine is not compatible with Windows 10. The software, apps, and drivers on your device don't work for the system. The app takes very little time to run the check and you don't need to do anything on your part. The results are separated into two sections; devices which lists incompatible hardware and Apps which will list incompatible apps.

Your PC might still be compatible but some devices will not and it's important to check which devices aren't, the reason being that sometimes a critical device might not be supported. The tool is back and is now significantly improved, and if it detects any incompatibilities with your PC, it will list them individually. But you can also prepare for an upgrade to Windows 11 by checking your PC's hardware and software capabilities by hand.

This approach is especially helpful if you've got a home-built PC that may have a Trusted Platform Module installed, but not enabled. So grab your current PC's specs and follow along as we go over the extensive lists of requirements that Microsoft has published. The brand new Windows 11 is here, and it comes with the most amazing features. The recent OS from Microsoft gets you new visual changes, compatibility with Android, interesting gaming-related qualities, and so on.

If you don't know that your Windows 10 PC or laptop is eligible for Windows 11 upgrade or not, you need to do your PC health check-up tool produced by Microsoft. Still, if the app appears that your laptop or PC is not compatible, so you should wait. Because Microsoft has revealed system requirements, on that basis, you can check the eligibility of your Windows 10 based laptop or desktop. The latest versions of all Adobe Creative Cloud products are compatible. This version of the operating system allows software to use 64-bit addresses to access hardware and can therefore access much larger memory spaces. In order to run successfully on Windows bit, all drivers must have native 64-bit support.

However, most 32-bit software applications can run within a Windows bit emulation layer. The following list of Dell Precision desktop computers that have been tested for update to Windows 10 Anniversary Update. The following list of Dell XPS laptops that have been tested for update to Windows 10 Anniversary Update. The following list of Dell XPS desktop computers that have been tested for update to Windows 10 Anniversary Update. The following list of Alienware laptops that have been tested for update to Windows 10 Anniversary Update.

The following list of Dell Precision desktop computers that have been tested for update to Windows 10 Creators Update. The following list of Dell XPS laptops that have been tested for update to Windows 10 Creators Update. The following list of Dell XPS desktop computers that have been tested for update to Windows 10 Creators Update. The following list of Alienware laptops that have been tested for update to Windows 10 Creators Update. The following list of Dell Precision desktop computers that have been tested for update to Windows 10 Fall Creators Update.

The following list of Dell XPS laptops that have been tested for update to Windows 10 Fall Creators Update. The following list of Dell XPS desktop computers that have been tested for update to Windows 10 Fall Creators Update. The following list of Dell Precision desktop computers that have been tested for update to Windows 10 April 2018 Update. The following list of Dell XPS laptops that have been tested for update to Windows 10 April 2018 Update. The following list of Dell XPS desktop computers that have been tested for update to Windows 10 April 2018 Update.